Projected STEM Shortages
It is common to encounter claims of a shortage or projected shortage of some number of millions of STEM (Science, Technology, Engineering and Mathematics) workers — sometimes phrased as millions of new jobs that may go unfilled due to the shortage of STEM workers. For example, the recent press release from Emerson Electric claiming a STEM worker shortage crisis includes the following paragraph:
While the survey found students today are twice as likely to study STEM fields compared to their parents, the number of roles requiring STEM expertise is growing at a rate that exceeds current workforce capacity. In manufacturing alone, the National Association of Manufacturing and Deloitte predict the U.S. will need to fill about 3.5 million jobs by 2025; yet as many as 2 million of those jobs may go unfilled, due to difficulty finding people with the skills in demand.
(Emphasis Added)
STEM shortage claimants often link the alleged shortage or projected shortage to poor K-12 education in the United States, often comparing US education critically to other nations such as Hong Kong, Singapore, and Finland.
How true are these seemingly alarming numbers?
Here are the numbers for United States students achieving a score of at least 3 out of 5, considered a passing grade — qualified, on the Advanced Placement (AP) Calculus exam, either the AB or the more advanced BC Calculus exam from the College Board. BC Calculus is equivalent to a full first year calculus course at a top STEM university or college such as MIT or Caltech. A score of 3 on an AP exam officially means “qualified.”
Calculus is a challenging college level quantitative course. Being rated as qualified or better in calculus is a substantial accomplishment. Calculus is taken by most STEM students regardless of specific STEM degree or profession. Mastering calculus demonstrates motivation, hard work, and innate ability. Calculus is required for many STEM degrees and professions. Calculus is “good to know” for nearly all STEM degrees and professions, even if not strictly required.
The AP exams are standardized tests taken by students throughout the United States, thus removing concerns about the quality of grades and certifications from differing institutions and teachers.
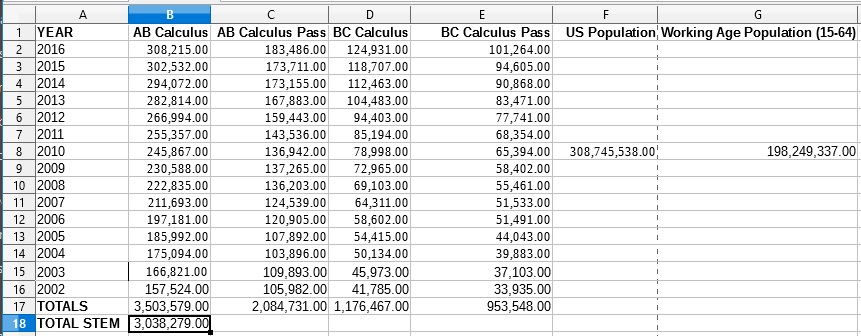
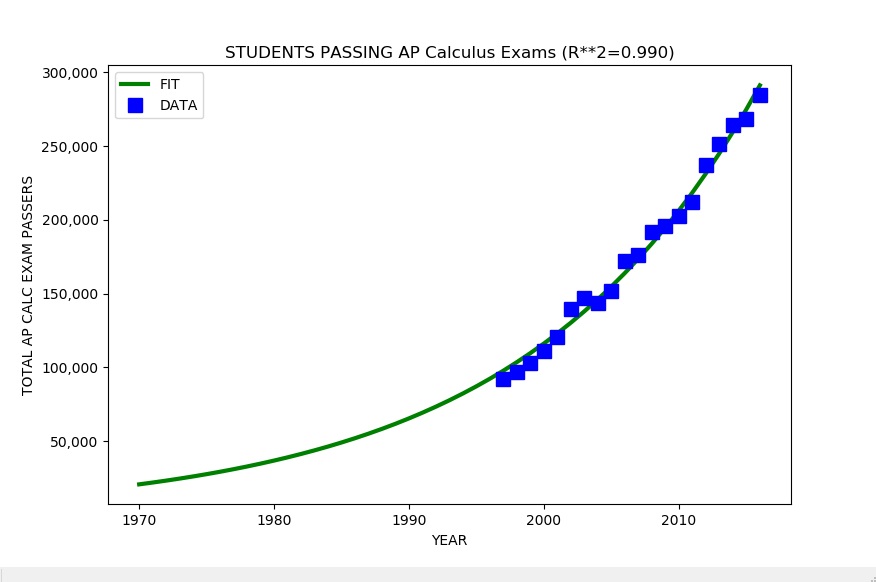
In 2016, about 284,000 students scored 3 or higher on the AP Calculus Exam, either the AB or the more advanced BC exam. In total, just over three million students scored 3 or higher on the AP Calculus exams from 2002 through 2016.
Here are the results of fitting a simple exponential growth model to the data to estimate the number of students who have received a score of 3 or higher on the AP Calculus Exam each year since 1970:
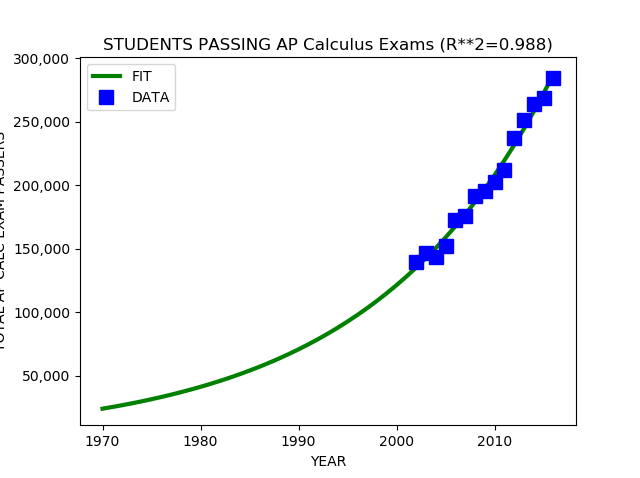
This model estimates a total of just over five (5) million students scoring 3 or higher on the AP Calculus Exams since 1970 (48 years ago). The model has a coefficient of determination of 0.988, meaning only 1.2 percent of the variation in the data is unexplained by the model. This is excellent agreement between the model and data.
The model predicts that about 4.2 million students will take the AP Calculus Exam and score 3 or higher between 2016 and 2026 (far more than the 2 million and 3.5 million numbers quoted in the Emerson press release). This is in addition to the over 3 million students the College Board says took the exam and scored 3 or better between 2002 and 2016 and the estimated 2 million between 1970 and 2002.
The United States produces many qualified STEM students at the K-12 level!
In 2016, the United States Bureau of Labor Statistics (BLS), arguably a more reliable and authoritative source than the Emerson press release, predicted the total number of STEM jobs would grow by 853,600 jobs from 2016 to 2026 ( a ten year prediction). This is considerably less than the four million students expected to score 3 or higher on AP Calculus between 2016 and 2026.
The BLS estimates that there were 7.3 million science and engineering workers employed in 2016, with a projected increase to 8.2 million in 2026.
The BLS also predicted that an additional 1.439 million scientists and engineers will exit the labor force due to factors such as retirement, death, and to care for family members . This is plausible assuming the science and engineering workforce has ages roughly uniformly distributed between 22 (typical college graduation age) and 65 (typically retirement age). In ten years, about a quarter of the science and engineering workforce might be expected to retire, die, or leave to care for family members. One quarter of 7.3 million is about 1.825 million.
Taken together overall growth (835,000) and retirements, deaths, etc. (about 1.8 million) give a total of about 2.635 million openings, considerably less than the predicted four million students who will take AP Calculus and score 3 or higher between 2016 and 2026. In fact, extrapolating the 284,000 students who scored 3 or higher on the AP Calculus Exam in 2016 forward for ten years with no growth (an unrealistic assumption) still gives 2.8 million students, more than the projected number of openings.
Occupational Transfers
However, the BLS then introduces a remarkable, if not bizarre additional category of projected “openings.” Here is John Sargent of the Congressional Research Service (CRS)’s discussion of the BLS projections:
In addition to the job openings created by growth in the number of jobs in S&E occupations, BLS projects that an additional 1. 439 million scientists and engineers will exit the labor force due to factors such as retirement, death, and to care for family members . This brings the number of S&E job openings created by job growth and those exiting the workforce to nearly 2.3 million. In addition, BLS projects that there will be an additional 3.7 million openings created by occupational transfers in S&E positions during this period, that is , workers in S&E occupations who leave their jobs to take jobs in different occupations, S&E or non-S&E. The BLS projections do not include data that allow for a quantitative analysis of how many new workers (those not in the labor market in 2016) will be required for openings created by job growth, labor force exits, and occupational transfers , as there is no detail to how many of the S&E openings are expected to be filled by workers transferring into these openings from S&E occupations and from non-S&E occupations (that is, some workers may transfer from one S&E occupation to another, some may transfer from an S&E occupations to a non-S&E occupations, and still others may transfer from a non-S&E occupation into an S&E occupations ) . According to BLS, the projections methodology allows for multiple occupational transfers from the same position during the 10-year projection period, but only one occupational transfer in a given year.
The BLS appears to be claiming that at least 3.7 million allegedly rare and difficult to find, highly paid STEM workers, over one half of currently employed STEM workers (7.3 million) will, for some unexplained reason — not retirement, death, or caring for a loved one — leave their profession!
This bizarre unexplained projection, now totaling six (6) million openings, finally manages to exceed the estimated four million students who will probably take AP Calculus and score 3 or better on the AP exam between 2016 and 2026.
Without the mysterious “occupational transfers,” the numbers actually suggest overproduction, a glut of STEM students at the K-12 level (more students taking the AP Calculus Exams and scoring 3 or higher than future openings).
The US Census found using the most common definition of STEM jobs, total STEM employment in 2012 was 5.3 million workers (immigrant and native), but there are 12.1 million STEM degree holders (immigrant and native). There are many more STEM degree holders than students who took AP Calculus and scored at least 3 on the exam! A majority of STEM degree holders do not work in STEM professions.
What should one make of this? The BLS seems to be assuming an extremely high turnover rate in STEM workers, with at least fifty percent dropping out or being pushed out in only ten years. This assumption may then be used to argue for a shortage! The shortage would be due entirely to the mysterious unexplained “occupational transfers.”
Conclusion
K-12 schools in the United States produce large numbers of highly qualified STEM students who routinely take and pass the AP Calculus exam, either the AB exam or the more advanced BC exam. Remarkably these top students alone are nearly able to fill all existing STEM jobs, not including guest workers on H1-B or other guest worker visas and not including many late bloomers who first take calculus in college or even graduate school.
NOTE: The raw data on numbers of students taking and passing the AP Calculus exams each year from 2002 to 2016 are in the Comma Separated Values (CSV) format and the Python model fitting script used in the analysis above are given in the Appendix below. The data follows the Python script.
(C) 2018 by John F. McGowan, Ph.D.
About Me
John F. McGowan, Ph.D. solves problems using mathematics and mathematical software, including developing gesture recognition for touch devices, video compression and speech recognition technologies. He has extensive experience developing software in C, C++, MATLAB, Python, Visual Basic and many other programming languages. He has been a Visiting Scholar at HP Labs developing computer vision algorithms and software for mobile devices. He has worked as a contractor at NASA Ames Research Center involved in the research and development of image and video processing algorithms and technology. He has published articles on the origin and evolution of life, the exploration of Mars (anticipating the discovery of methane on Mars), and cheap access to space. He has a Ph.D. in physics from the University of Illinois at Urbana-Champaign and a B.S. in physics from the California Institute of Technology (Caltech).
Appendix
estimate_k12_stem.py
#
# estimate total production of STEM students at the
# K-12 level (pre-college)
#
# data and model for number of students who pass the
# AP Calculus exams (both AB and BC) from the College
# Board each year (data from 2002 to 2016)
#
# estimate total production of STEM students by K-12
# education from 1970 to 2016 (about 5 million estimated)
#
# versus about 12.1 million STEM degree holders in 2014
# and 5.3 million actual employed STEM workers in 2014
#
# Source: https://cis.org/There-STEM-Worker-Shortage
#
# (C) 2018 by John F. McGowan, Ph.D. (ceo@mathematical-software.com)
#
#
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from mpl_toolkits.mplot3d import Axes3D
import scipy.optimize as opt
import pandas as pd
df = pd.read_csv(“AP Calculus Totals by Year.csv”)
df.dropna()
ab_str = df.values[:,2]
bc_str = df.values[:,4]
ab = np.zeros(ab_str.shape)
bc = np.zeros(bc_str.shape)
index = 0
for val in ab_str.ravel():
if isinstance(val, str):
ab[index] = np.float(val.replace(‘,’,”))
index += 1
index = 0
for val in bc_str.ravel():
if isinstance(val, str):
bc[index] = np.float(val.replace(‘,’, ”))
index += 1
temp = ab + bc
total = temp[:-2]
years_str = df.values[0:15,0]
years = np.zeros(years_str.shape)
for index in range(years.size):
years[index] = np.float(years_str[index])
START_YEAR = 1970
def my_exp(x, *p):
“””
exponential model
“””
return p[0]*np.exp(p[1]*(x – START_YEAR))
p_start = [ 50000.0, 0.01 ]
popt, pcov = opt.curve_fit(my_exp, years, total, p_start)
print(popt)
STOP_YEAR = 2016
NYEARS = (STOP_YEAR – START_YEAR + 1)
years_fit = np.linspace(START_YEAR, STOP_YEAR, NYEARS)
n_fit = my_exp(years_fit, *popt)
n_pred = my_exp(years, *popt)
r2 = 1.0 – (n_pred – total).var()/total.var()
r2_str = “%4.3f” % r2
cum_total = n_fit.sum()
# to match BLS projections
future_years = np.linspace(2016, 2026, 11)
assert future_years.size == 11
future_students = my_exp(future_years, *popt)
# https://fas.org/sgp/crs/misc/R43061.pdf
#
# The U.S. Science and Engineering Workforce: Recent, Current,
# and Projected Employment, Wages, and Unemployment
#
# by John F. Sargent Jr.
# Specialist in Science and Technology Policy
# November 2, 2017
#
# Congressional Research Service 7-5700 www.crs.gov R43061
#
# “In 2016, there were 6.9 million scientists and engineers (as
# defined in this report) employed in the United States, accounting
# for 4.9 % of total U.S. employment.”
#
# BLS astonishing/bizarre projections for 2016-2026
# “The Bureau of Labor Statistics (BLS) projects that the number of S&E
# jobs will grow by 853,600 between 2016 and 2026 , a growth rate
# (1.1 % CAGR) that is somewhat faster than that of the overall
# workforce ( 0.7 %). In addition, BLS projects that 5.179 million
# scientists and engineers will be needed due to labor force exits and
# occupational transfers (referred to collectively as occupational
# separations ). BLS projects the total number of openings in S&E due to growth ,
# labor force exits, and occupational transfers between 2016 and 2026 to be
# 6.033 million, including 3.477 million in the computer occupations and
# 1.265 million in the engineering occupations.”
# NOTE: This appears to project 5.170/6.9 or 75 percent!!!! of current STEM
# labor force LEAVE THE STEM PROFESSIONS by 2026!!!!
# “{:,}”.format(value) to specify the comma separated thousands format
#
print(“TOTAL Scientists and Engineers 2016:”, 6.9e6)
print(“ESTIMATED TOTAL IN 2016 SINCE “, START_YEAR, \
“{:,}”.format(cum_total))
print(“TOTAL FROM 2002 to 2016 (College Board Data) “, \
“{:,}”.format(total.sum()))
print(“ESTIMATED FUTURE STUDENTS (2016 to 2026):”, \
“{:,}”.format(future_students.sum()))
f1 = plt.figure()
ax = plt.gca()
ax.get_yaxis().set_major_formatter(
ticker.FuncFormatter(lambda x, p: format(int(x), ‘,’)))
plt.plot(years_fit, n_fit, ‘g’, linewidth=3, label=’FIT’)
plt.plot(years, total, ‘bs’, markersize=10, label=’DATA’)
plt.legend()
plt.title(‘STUDENTS PASSING AP Calculus Exams (R**2=’ \
+ r2_str + “)”)
plt.xlabel(‘YEAR’)
plt.ylabel(‘TOTAL AP CALC EXAM PASSERS’)
plt.show()
AP Calculus Totals by Year.csv
YEAR,AB Calculus,AB Calculus Pass,BC Calculus,BC Calculus Pass,US Population,Working Age Population (15-64)
2016,"308,215.00","183,486.00","124,931.00","101,264.00",,
2015,"302,532.00","173,711.00","118,707.00","94,605.00",,
2014,"294,072.00","173,155.00","112,463.00","90,868.00",,
2013,"282,814.00","167,883.00","104,483.00","83,471.00",,
2012,"266,994.00","159,443.00","94,403.00","77,741.00",,
2011,"255,357.00","143,536.00","85,194.00","68,354.00",,
2010,"245,867.00","136,942.00","78,998.00","65,394.00","308,745,538.00","198,249,337.00"
2009,"230,588.00","137,265.00","72,965.00","58,402.00",,
2008,"222,835.00","136,203.00","69,103.00","55,461.00",,
2007,"211,693.00","124,539.00","64,311.00","51,533.00",,
2006,"197,181.00","120,905.00","58,602.00","51,491.00",,
2005,"185,992.00","107,892.00","54,415.00","44,043.00",,
2004,"175,094.00","103,896.00","50,134.00","39,883.00",,
2003,"166,821.00","109,893.00","45,973.00","37,103.00",,
2002,"157,524.00","105,982.00","41,785.00","33,935.00",,
TOTALS,"3,503,579.00","2,084,731.00","1,176,467.00","953,548.00",,
TOTAL STEM,"3,038,279.00",,,,,