In the 1997 movie Wag the Dog a mysterious consultant played by Robert DeNiro and a Hollywood producer/campaign contributor played by Dustin Hoffman fake a war in Albania complete with a computer generated terrorism video produced by movie biz special effects wizards to divert public attention from a sex scandal engulfing a Bill Clinton-like President who is running for reelection. The phony war succeeds despite several snafus and a brief rebellion by the CIA. The President is reelected amidst a surge of war fever and patriotism. How well do wars work in the real world?

The most spectacular boost in Presidential approval ratings due to a war followed the September 11, 2001 terrorist attacks that killed about 3,000 people on US soil, probably the largest single day massacre in US history both in absolute numbers and fraction of the population. (The few day Santee massacre of settlers by Dakota Sioux Indians in Minnesota in 1862 probably killed a larger fraction of the population at the time.) President George W. Bush and the Republicans seem to have benefited electorally from the subsequent “war on terror” in the 2002 and 2004 elections.
However, historically the effect of wars and national security events such as the successful launch of the Sputnik I (October 4, 1957) and II (November 3, 1957) satellites by the Soviet Union on Presidential approval ratings and electoral prospects is much more varied. Sputnik II is significant because the second satellite was large enough to carry a nuclear bomb unlike the beach ball sized Sputnik I.
Truman and the Korean War

President Harry Truman’s approval ratings had been declining for over a year prior to the start of the Korean War. He may have experienced a slight bump for a couple of months (see plot above) followed by further decline.
Eisenhower and the End of the Korean War

Like most new Presidents, Dwight Eisenhower experienced a big “honeymoon” jump over his predecessor Harry Truman. There is little sign he either benefited or suffered from the end of the Korean War.
Eisenhower and Sputnik I and II

Eisenhower’s approval ratings had been declining for almost a year when the Soviet Union successfully launched the first satellite Sputnik I on October 4, 1957. This was followed by the much larger Sputnik II on November 3, 1957 — theoretically capable of carrying a nuclear bomb. Although Sputnik I and II were big news stories and led to a huge reaction in the United States, there is no clear effect on Eisenhower’s approval ratings. He rebounded in early 1958 and left office as one of the most popular Presidents.
However, Eisenhower, his administration, and his Vice President Richard Nixon who ran for President in 1960 were heavily criticized over the missile race with the Soviet Union due to Sputnik. Sputnik was followed by high profile, highly publicized failures of US attempts to launch satellites. Administration claims that the Soviet Union was in fact behind the US in the race to build nuclear missiles were widely discounted, although this seems to have been true.
John F. Kennedy ran successfully for President in 1960 claiming the notorious “missile gap” and calling for a massive nuclear missile build up, winning narrowly over Nixon in a bitterly contested election with widespread allegations of voting fraud in Texas and Chicago. Eisenhower’s famous farewell address coining (or at least popularizing) the phrase “military industrial complex” was a reaction to the controversy over Sputnik and the nuclear missile program.
Kennedy and the Cuban Missile Crisis

President Kennedy experienced a large boost in previously declining approval ratings during and after the Cuban Missile Crisis in October of 1962. This is often considered the closest the world has come to a nuclear war until the recent confrontation with Russia over the Ukraine. It also occurred only weeks before the mid-term elections in November of 1962.
Johnson and the Vietnam War

The Vietnam War ultimately destroyed President Lyndon Johnson’s approval ratings with the aging President declining to run for another term in 1968 amidst massive protests and challenges from Senator Robert Kennedy and others. There is actually little evidence of a boost from the Gulf of Tonkin incidents in August of 1964 and the subsequent Gulf of Tonkin resolution leading to the larger war.
President Johnson ran on a “peace” platform, successfully portraying the Republican candidate Senator Barry Goldwater of Arizona as a nutcase warmonger. Yet, Johnson — at the same time — visibly escalated the US involvement in the then obscure nation of Vietnam in August only a few months before the Presidential election in 1964.
Ford and the End of the Vietnam War

The end of the Vietnam War (April 30, 1975) seems to have boosted President Gerald Ford’s approval ratings significantly, about ten percent. Nonetheless, he was defeated by Jimmy Carter in 1976.
Carter and the Iran Hostage Crisis

President Jimmy Carter experienced a substantial boost in approval ratings when “students” took over the US Embassy in Tehran, Iran on November 4, 1979, holding the embassy staff hostage for 444 days. This lasted a few months, followed by a rapid decline back to Carter’s previous dismal approval ratings. The failure to rescue or secure the release of the hostages almost certainly contributed to Carter’s loss the Ronald Reagan in 1980.
George H.W. Bush and Iraq War I (Operation Desert Storm)

President George Herbert Walker Bush experienced a large boost in approval ratings at the end of the first Iraq War followed by a large and rapid decline, losing to Bill Clinton in 1992.
President George Bush, September 11, Iraq War II, and Afghanistan are discussed at the start of this article — overall probably the clearest boost in approval and electoral performance from a war at least since World War II.
Biden and Ukraine
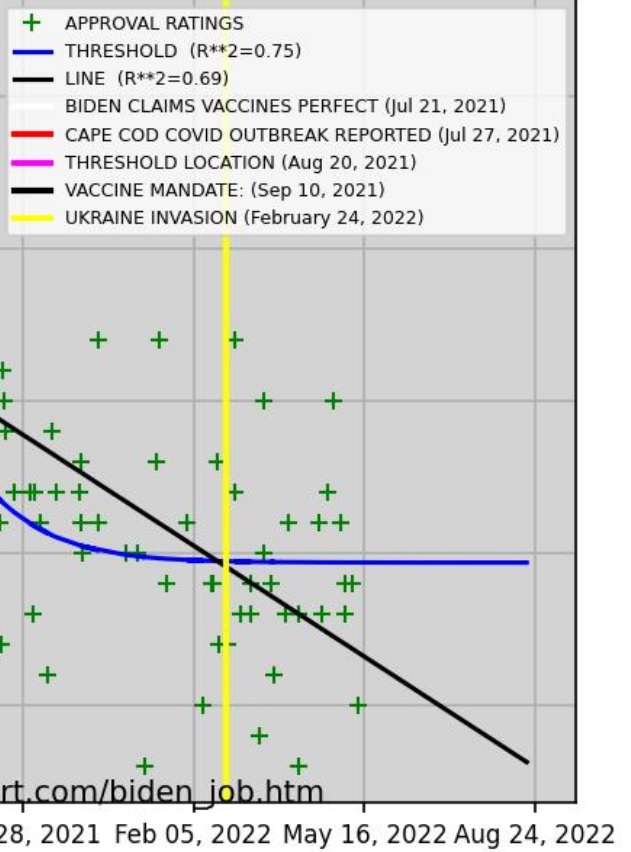
As of June 16, 2022, President Joe Biden’s approval ratings have continued to decline since the February 24, 2022 invasion of Ukraine by Russia. There is not the slightest sign of any boost.
Conclusion
Despite the folk tradition epitomized by the movie Wag the Dog that wars boost a President’s approval and electoral prospects — at least initially — history shows mixed results. Some wars have clearly boosted the President’s prospects, notably after September 11, and others have done nothing or even contributed to further decline. Korea, for example, seems to have only contributed to President Truman’s marked decline and the loss to Eisenhower in 1952.
Probably the lesson is to avoid wars and focus on resolving substantive domestic economic problems.
(C) 2022 by John F. McGowan, Ph.D.
About Me
John F. McGowan, Ph.D. solves problems using mathematics and mathematical software, including developing gesture recognition for touch devices, video compression and speech recognition technologies. He has extensive experience developing software in C, C++, MATLAB, Python, Visual Basic and many other programming languages. He has been a Visiting Scholar at HP Labs developing computer vision algorithms and software for mobile devices. He has worked as a contractor at NASA Ames Research Center involved in the research and development of image and video processing algorithms and technology. He has published articles on the origin and evolution of life, the exploration of Mars (anticipating the discovery of methane on Mars), and cheap access to space. He has a Ph.D. in physics from the University of Illinois at Urbana-Champaign and a B.S. in physics from the California Institute of Technology (Caltech).