“Half the money I spend on advertising is wasted; the trouble is I don’t know which half.”
John Wanamaker, (attributed)
US department store merchant (1838 – 1922)
Between $190 billion and $270 billion is spent on advertising in the United States each year (depending on source). It is often hard to tell whether the advertising boosts sales and profits. This is caused by the unpredictability of individual sales and in many cases the other changes in the business and business environment occurring in addition to the advertising. In technical terms, the evaluation of the effect of advertising on sales and profits is often a multidimensional problem.
Many common metrics such as the number of views, click through rates (CTR), and others do not directly measure the change in sales or profits. For example, an embarrassing or controversial video can generate large numbers of views, shares, and even likes on a social media site and yet cause a sizable fall in sales and profits.
Because individual sales are unpredictable, it is often difficult or impossible to tell whether a change in sales is caused by advertising, simply due to chance alone or some combination of advertising and luck.
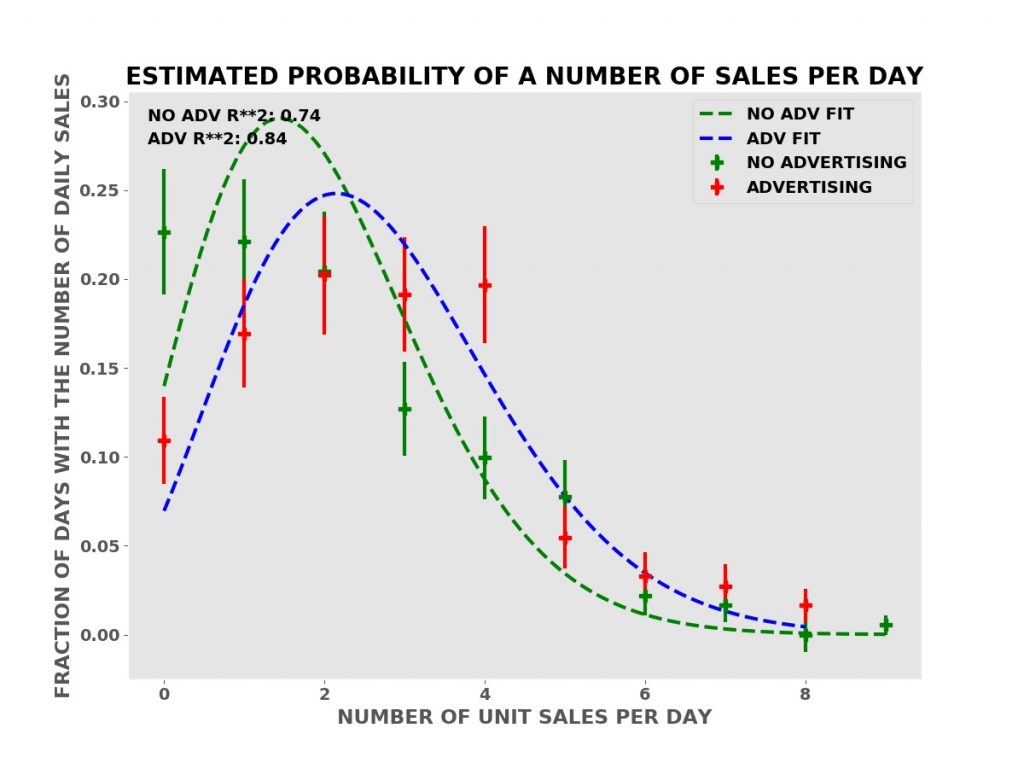
The plot below shows the simulated daily sales for a product or service with a price of $90.00 per unit. Initially, the business has no advertising, relying on word of mouth and other methods to acquire and retain customers. During this “no advertising” period, an average of three units are sold per day. The business then contracts with an advertising service such as Facebook, Google AdWords, Yelp, etc. During this “advertising” period, an average of three and one half units are sold per day.
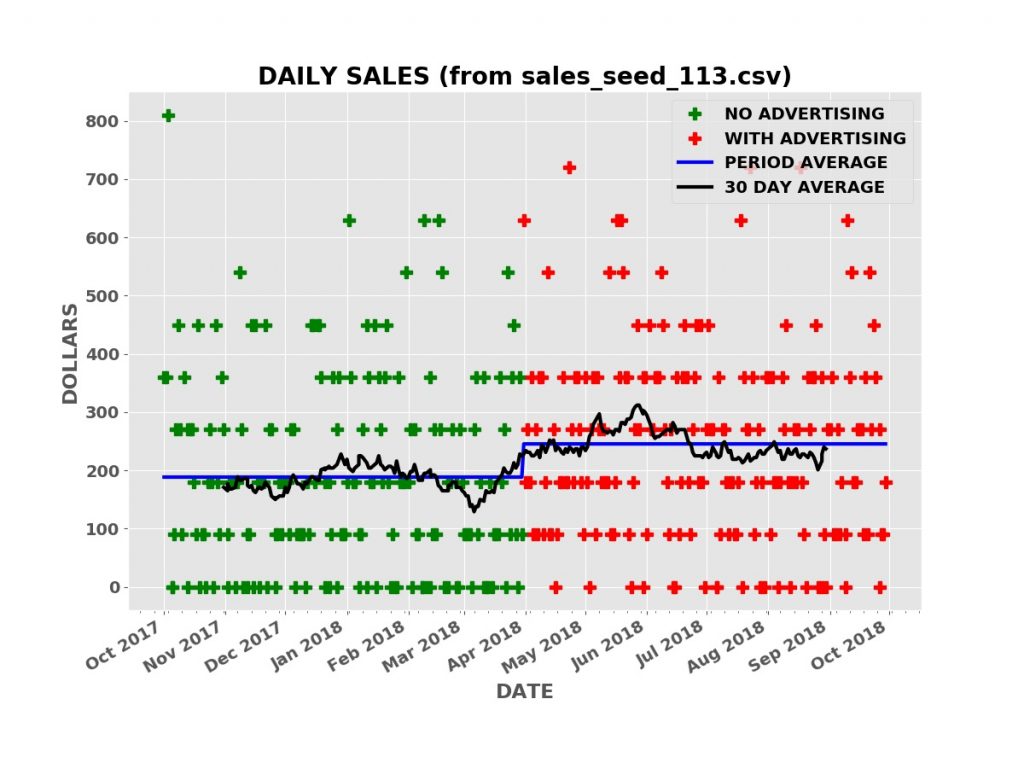
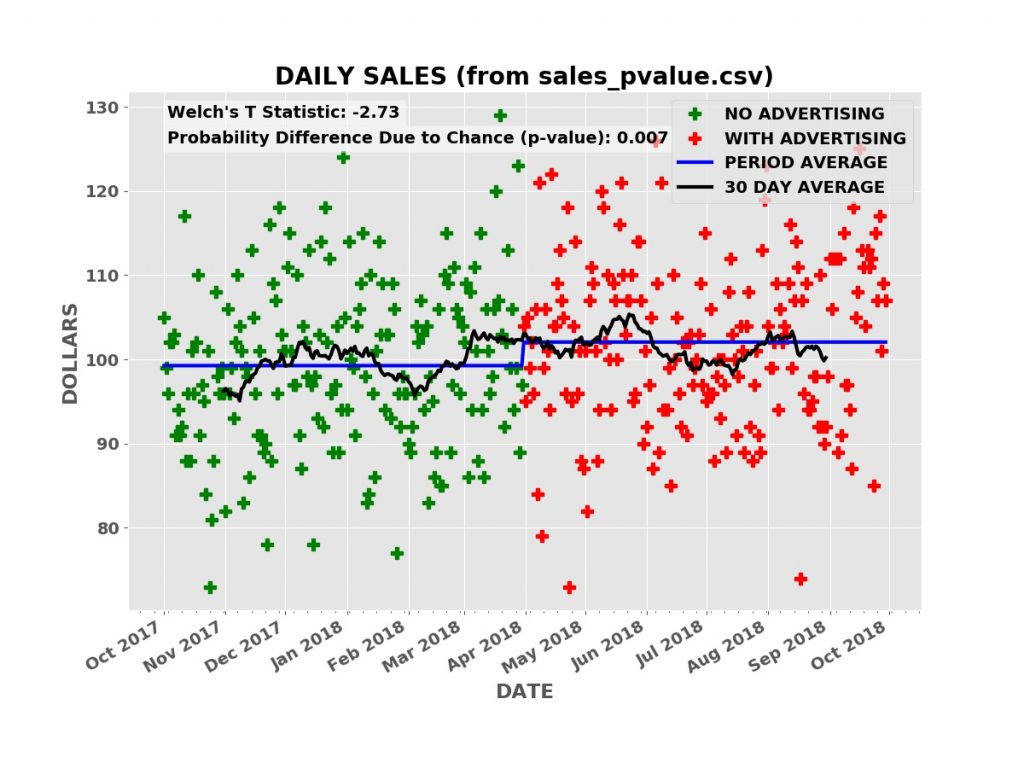
The raw daily sales data is impossible to interpret. Even looking at the thirty day moving average of daily sales (the black line), it is far from clear that the advertising campaign is boosting sales.
Taking the average daily sales over the “no advertising” period, the first six months, and over the “advertising” period (the blue line), the average daily sales was higher during the advertising period.
Is the increase in sales due to the advertising or random chance or some combination of the two causes? There is always a possibility that the sales increase is simply due to chance. How much confidence can we have that the increase in sales is due to the advertising and not chance?
This is where statistical methods such as Student’s T test, Welch’s T test, mathematical modeling and computer simulations are needed. These methods compute the effectiveness of the advertising in quantitative terms. These quantitative measures can be converted to estimates of future sales and profits, risks and potential rewards, in dollar terms.
Measuring the Difference Between Two Random Data Sets
In most cases, individual sales are random events like the outcome of flipping a coin. Telling whether sales data with and without advertising is the same is similar to evaluating whether two coins have the same chances of heads and tails. A “fair” coin is a coin with an equal chance of giving a head or a tail when flipped. An “unfair” coin might have a three fourths chance of giving a head and only a one quarter chance of giving a tail when flipped.
If I flip each coin once, I cannot tell the difference between the fair coin and the unfair coin. If I flip the two coins ten times, on average I will get five heads from the fair coin and seven and one half (seven or eight) heads from the unfair coin. It is still hard to tell the difference. With one hundred times, the fair coin will average fifty heads and the unfair coin seventy-five heads. There is still a small chance that the seventy five heads came from a fair coin.
The T statistics used in Student’s T test (Student was a pseudonym used by statistician William Sealy Gossett) and Welch’s T test, a more advanced T test, are measures of the difference in a statistical sense between two random data sets, such as the outcome of flipping coins one hundred times. The larger the T statistic the more different the two random data sets in a statistical sense.

Student’s T test and Welch’s T test convert the T statistics into probabilities that the difference between the two data sets (the “no advertising” and “advertising” sales data in our case) is due to chance. Student’s T test and Welch’s T test are included in Excel and many other financial and statistical programs.
The plot below is a histogram (bar chart) of the number of simulations with a Welch’s T statistic value. In these simulations, the advertising has no effect on the daily sales (or profits). The advertising has no effect is the null hypothesis in the language of classical statistics.
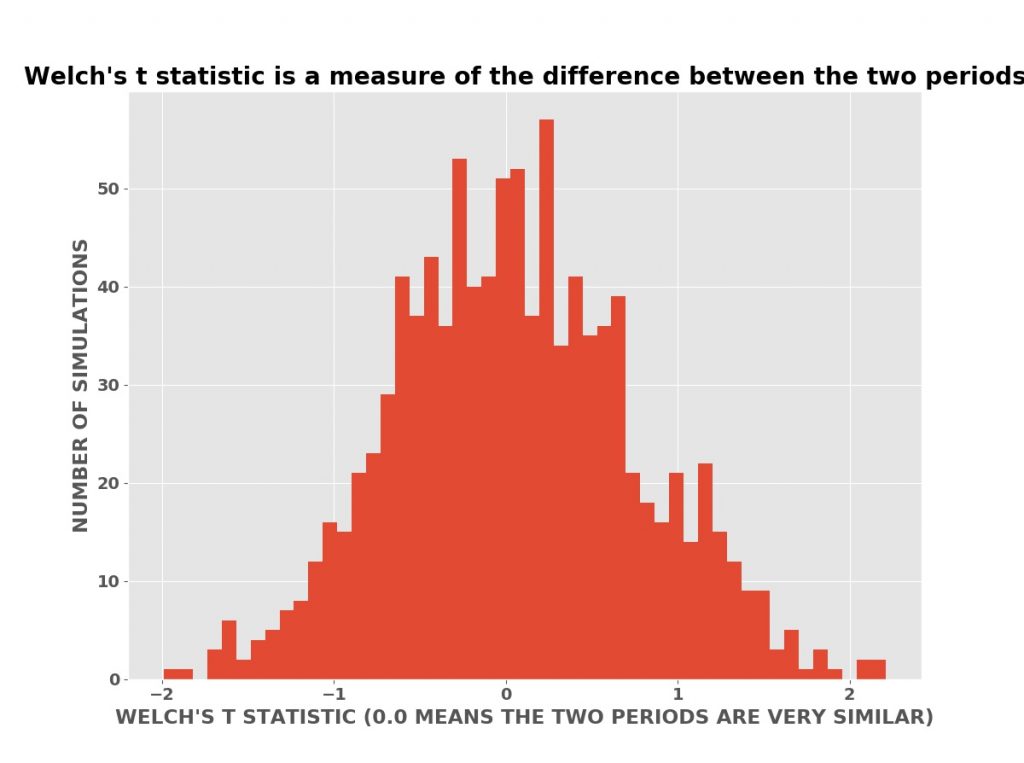
Welch was able to derive a mathematical formula for the expected distribution — shape of this histogram — using calculus. The mathematical formula could then be evaluated quickly with pencil and paper or an adding machine, the best available technology of his time (the 1940’s).
To derive his formula using calculus, Welch had to assume that the data had a Bell Curve (Normal or Gaussian) distribution. This is at best only approximately true for the sales data above. The distribution of daily sales in the simulated data is actually the Poisson distribution. The Poisson distribution is a better model of sales data and approximates the Bell Curve as the number of sales gets larger. This is why Welch’s T test is often approximately valid for sales data.
Many methods and tests in classical statistics assume a Bell Curve (Normal or Gaussian) distribution and are often approximately correct for real data that is not Bell Curve data. We can compute better, more reliable results with computer simulations using the actual or empirical probability distributions — shown below.
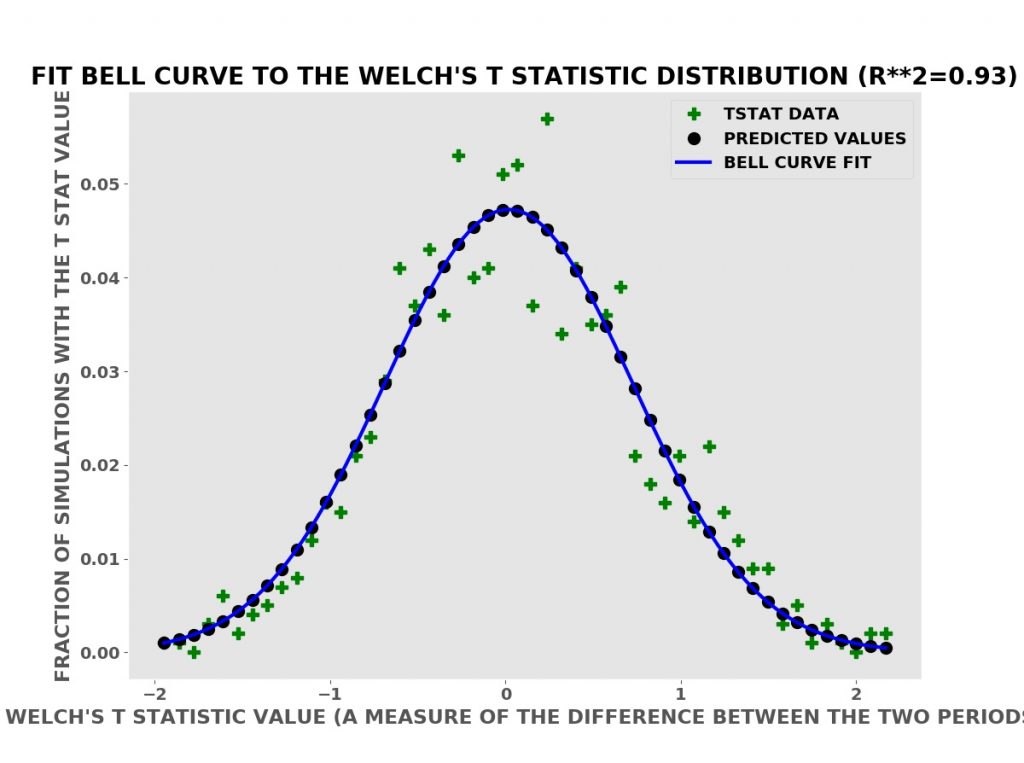
More precisely, naming one data set the reference data and the other data set the test data, the T test computes the probability that the test data is due to a chance variation in the process that produced the reference data set. In the advertising example above, the “no advertising” period sales data is the reference data and the “advertising” sales data is the test data. Roughly this probability is the fraction of simulations in the Welch’s T statistic histogram that have a T statistic larger (or smaller for a negative T statistic) than the measured T statistic for the actual data. This probability is known as a p-value, a widely used statistic pioneered by Ronald Fisher.

The p-value has some obvious drawbacks for a business evaluating the effectiveness of advertising. At best it only tells us the probability that the advertising boosted sales or profits, not how large the boost was nor the risks. Even if on average the advertising boosts sales, what is the risk the advertising will fail or the sales increase will be too small to recover the cost of the advertising?
Fisher worked for Rothamsted Experimental Station in the United Kingdom where he wanted to know whether new breeds of crops, fertilizers, or other new agricultural methods increased yields. His friend and colleague Gossett worked for the Guinness beer company where he was working on improving yields and quality of beer. In both cases, they wanted to know whether a change in the process had a positive effect, not the size of the effect. Without modern computers — using only pencil and paper and adding machines — it was not practical to perform simulations as we can easily today.
Welch’s T statistic has a value of -3.28 for the above sales data. This is in fact lower than nearly all the simulations in the histogram. It is very unlikely the boost in sales is due to chance. The p-value from Welch’s T test for the advertising data above — computed using Welch’s mathematical formula — is only 0.001 (one tenth of one percent). Thus it is very likely the boost in sales is caused by the advertising and not random chance. Note that this does not tell us if the size of the boost, whether the advertising is cost effective, or the risk of the investment.
Sales and Profit Projections Using Computer Simulations
We can do much better than Student’s T test and Welch’s T test by using computer simulations based on the empirical probabilities of sales from the reference data — the “no advertising” period sales data. The simulations use random number generators to simulate the random nature of individual sales.
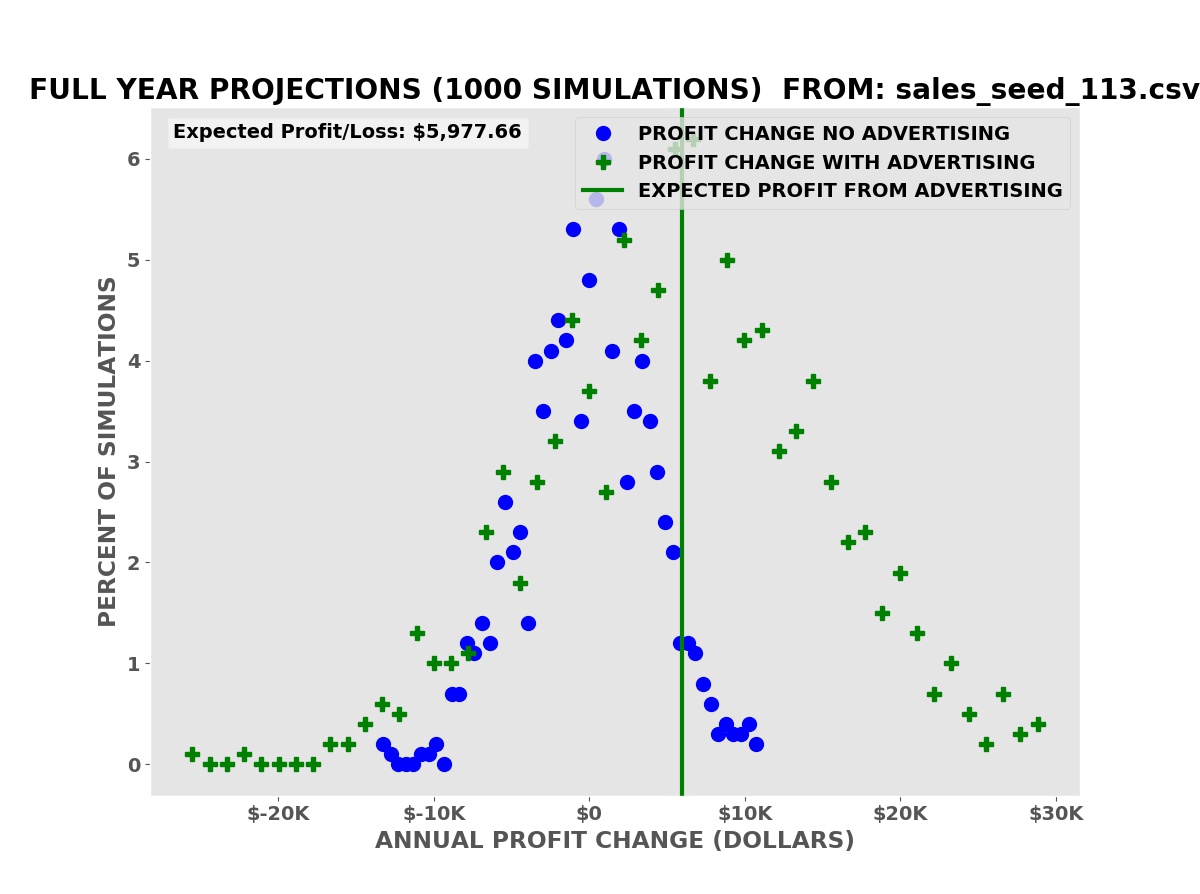
In these simulations, we simulate one year of business operations with advertising many times — one-thousand in the examples shown — using the frequency of sales from the period with advertising. We also simulate one year of business operations without the advertising, using the frequency of sales from the period without advertising in the sales data.
We compute the annual change in the profit relative to the corresponding period — with or without advertising — in the sales data for each simulated year of business operations.
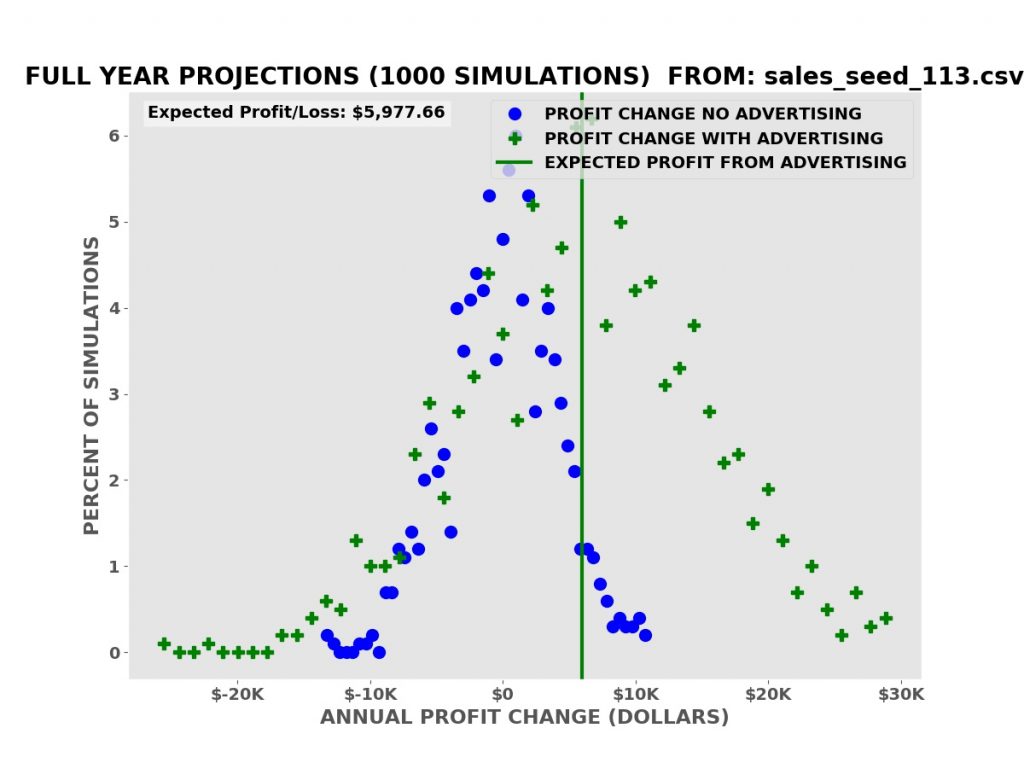
The simulations show that we have an average expected increase in profit of $5,977.66 over one year (our annual advertising cost is $6,000.00). It also shows that despite this there is a risk of a decrease in profits, some greater than the possible decreases with no advertising.
A business needs to know both the risks — how much money might be lost in a worst case — and the rewards — the average and best possible returns on the advertising investment.
Since sales are a random process like flipping a coin or throwing dice, there is a risk of a decline in profits or actual losses without the advertising. The question is whether the risk with advertising is greater, smaller, or the same. This is known as differential risk.
The Problem with p-values
This is a concrete example of the problem with p-values for evaluating the effectiveness of advertising. In this case, the advertising increases the average daily sales from 100 units per day to 101 units per day. Each unit costs one dollar (a candy bar for example).
The p-value from Welch’s T test is 0.007 (seven tenths of one percent). The advertising is almost certainly effective but the boost in sales is much less than the cost of the advertising:
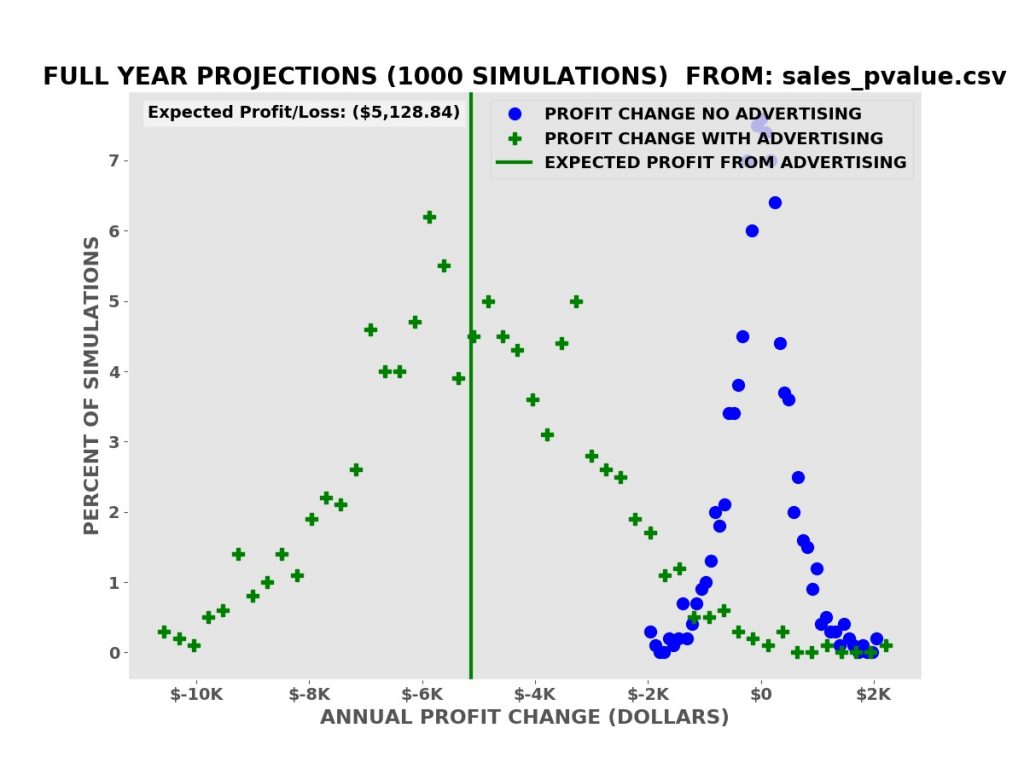
The average expected decline in profits over the simulations is $5,128.84.
The p-value is not a good estimate of the potential risks and rewards of investing in advertising. Sales and profit projections from computer simulations based on a mathematical model derived from the reference sales data are a better (not perfect) estimate of the risks and rewards.
Multidimensional Sales Data
The above examples are simple cases where the only change is the addition of the advertising. There are no price changes, other advertising or marketing expenses, or other changes in business or economic conditions. There are no seasonal effects in the sales.
Student’s T test, Welch’s T test, and many other statistical tests are designed and valid only for simple controlled cases such as this where there is only one change between the reference and test data. These tests were well suited to data collected at the Rothamsted Experimental Station, Guinness breweries, and similar operations.
Modern businesses purchasing advertising from Facebook, other social media services, and modern media providers (e.g. the New York Times) face more complex conditions with many possible input variables (unit price, weather, unemployment rate, multiple advertising services, etc.) changing frequently or continuously.
For these, financial analysts need to extract predictive multidimensional mathematical models from the data and then perform similar simulations to evaluate the effect of advertising on sales and profits.
Example Software
The AdEvaluator™ software used in these examples is free open source software (FOSS) developed using the Anaconda Python 3 distribution. It is available under the GNU General Public License Version 3.
AdEvaluator can be downloaded here.
Disclaimer
AdEvaluator™ is designed for cases with a single product or service with a constant unit price during both periods. AdEvaluator™ needs a reference period without the new advertising and a test period with the new advertising campaign. The new advertising campaign should be the only significant change between the two periods. AdEvaluator™ also assumes that the probability of the daily sales is independent and identically distributed during each period. This is not true in all cases. Exercise your professional business judgement whether the results of the simulations are applicable to your business.
This program comes with ABSOLUTELY NO WARRANTY; for details use -license option at the command line or select Help | License… in the graphical user interface (GUI). This is free software, and you are welcome to redistribute it under certain conditions.
We are developing a professional version of AdEvaluator™ for multidimensional cases. This version uses our Math Recognition™ technology to automatically identify good multidimensional mathematical models.
The Math Recognition™ technology is applicable to many types of data, not just sales and advertising data. It can for example be applied to complex biological systems such as the blood coagulation system which causes heart attacks and strokes when it fails. According the US Centers for Disease Control (CDC) about 633,000 people died from heart attacks and 140,000 from strokes in 2016.
Conclusion
It is often difficult to evaluate whether advertising is boosting sales and profits, despite the ready availability of sales and profit data for most businesses. This is caused by the unpredictable nature of individual sales and frequently by the complex multidimensional business environment where price changes, economic downturns and upturns, the weather, and other factors combine with the advertising to produce a confusing picture.
In simple cases with a single change, the addition of the new advertising, Student’s T test, Welch’s T test and other methods from classical statistics can help evaluate the effect of the advertising on sales and profits. These statistical tests can detect an effect but provide no clear estimate of the magnitude of the effect on sales and profits and the financial risks and rewards.
Sales and profit projections based on computer simulations using the empirical probability of sales from the actual sales data can provide quantitative estimates of the effect on sales and profits, including estimates of the financial risks (chance of losing money) and the financial rewards (typical and best case profits).
(C) 2018 by John F. McGowan, Ph.D.
About Me
John F. McGowan, Ph.D. solves problems using mathematics and mathematical software, including developing gesture recognition for touch devices, video compression and speech recognition technologies. He has extensive experience developing software in C, C++, MATLAB, Python, Visual Basic and many other programming languages. He has been a Visiting Scholar at HP Labs developing computer vision algorithms and software for mobile devices. He has worked as a contractor at NASA Ames Research Center involved in the research and development of image and video processing algorithms and technology. He has published articles on the origin and evolution of life, the exploration of Mars (anticipating the discovery of methane on Mars), and cheap access to space. He has a Ph.D. in physics from the University of Illinois at Urbana-Champaign and a B.S. in physics from the California Institute of Technology (Caltech).