It is common to encounter claims of a “desperate” or “severe” shortage of STEM (Science, Technology, Engineering, and Mathematics) workers, either current or projected, usually from employers of STEM workers. These claims are perennial and date back at least to the 1940’s after World War II despite the huge number of STEM workers employed in wartime STEM projects (the Manhattan Project that developed the atomic bomb, military radar, code breaking machines and computers, the B-29 and other high tech bombers, the development of penicillin, K-rations, etc.). This article takes a look at the STEM degree numbers in the National Science Foundation’s Science and Engineering Indicators 2018 report.
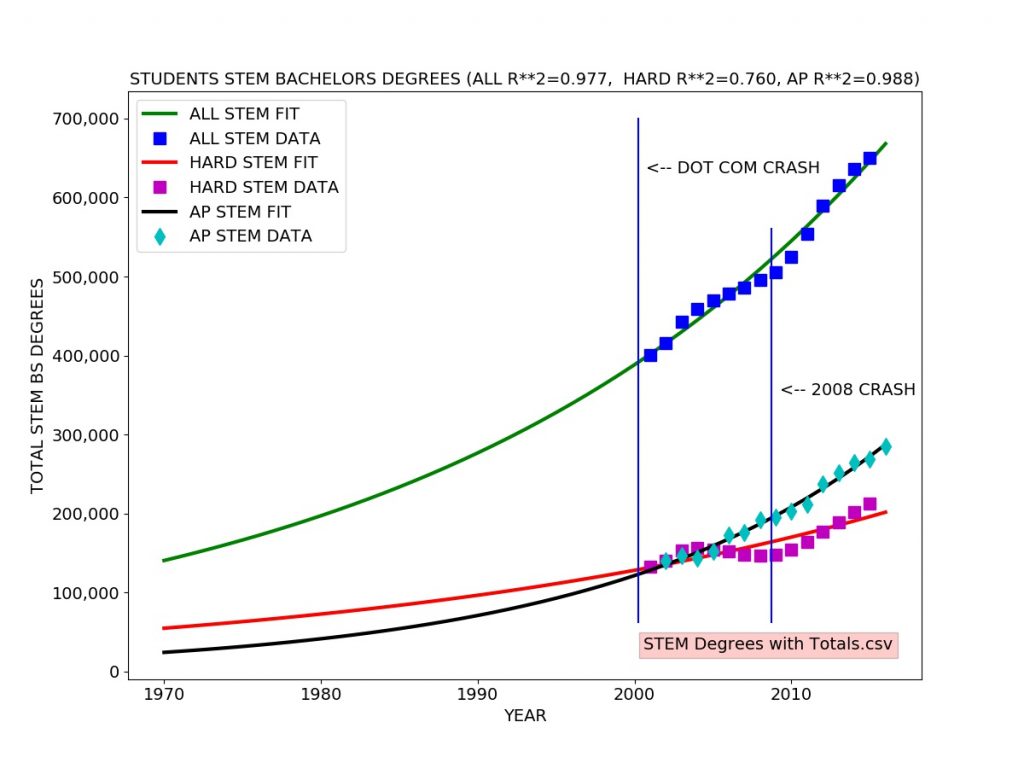
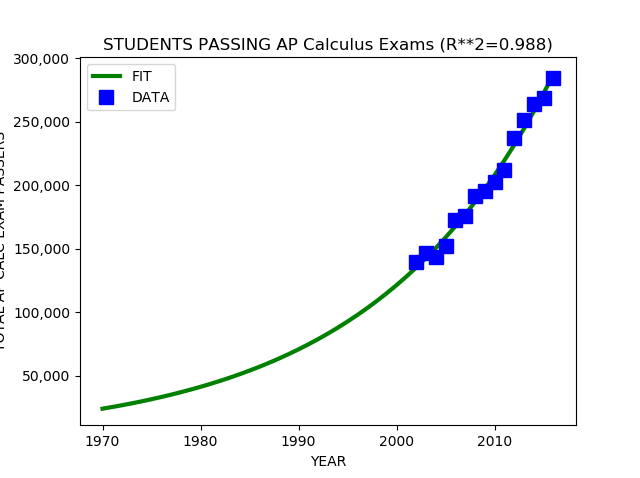
I looked at the total Science and Engineering bachelors degrees granted each year which includes degrees in Social Science, Psychology, Biological and agricultural sciences as well as hard core Engineering, Computer Science, Mathematics, and Physical Sciences. I also looked specifically at the totals for “hard” STEM degrees (Engineering, Computer Science, Mathematics, and Physical Sciences). I also included the total number of K-12 students who pass (score 3,4, or 5 out of 5) on the Advanced Placement (AP) Calculus Exam (either the AB exam or the more advanced BC exam) each year.
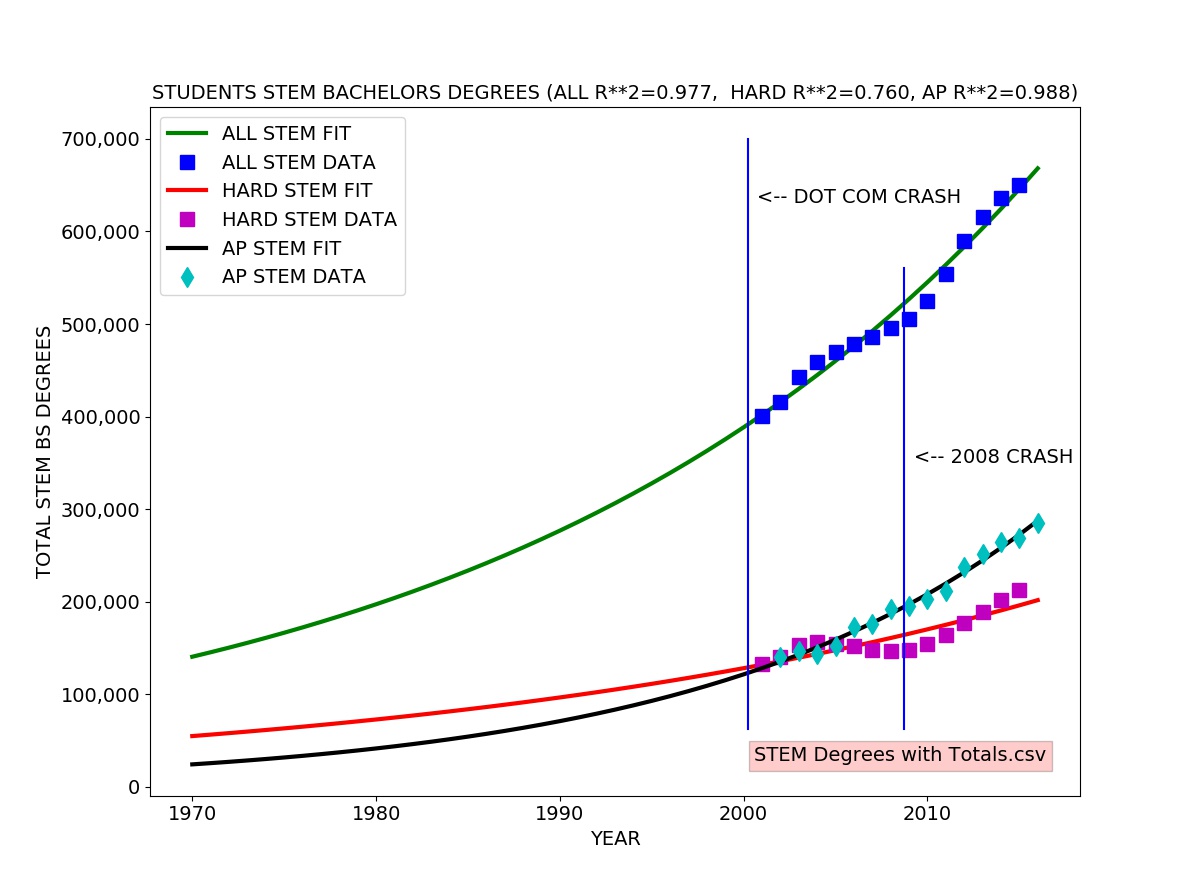
I fitted an exponential growth model to each data series. The exponential growth model fits well to the total STEM degrees and AP passing data. The exponential growth model roughly agrees with the hard STEM degree data, but there is a clear difference, reflected in the coefficient of determination (R-SQUARED) of 0.76 meaning the model explains about 76 percent of the variation in the data.
One can easily see the the number of hard STEM degrees significantly exceeds the trend line in the early 00’s (2000 to about 2004) and drops well below from 2004 to 2008, rebounding in 2008. This probably reflects the surge in CS degrees specifically due to the Internet/dot com bubble (1995-2001).
There appears to be a lag of about four years between the actual dot com crash usually dated to a stock market drop in March of 2000 and the drop in production of STEM bachelor’s degrees in about 2004.
Analysis results:
TOTAL Scientists and Engineers 2016: 6,900,000 ALL STEM Bachelor's Degrees ESTIMATED TOTAL IN 2016 SINCE 1970: 15,970,052 TOTAL FROM 2001 to 2015 (Science and Engineering Indicators 2018) 7,724,850 ESTIMATED FUTURE STUDENTS (2016 to 2026): 8,758,536 ANNUAL GROWTH RATE: 3.45 % US POPULATION GROWTH RATE (2016): 0.7 % HARD STEM DEGREES ONLY (Engineering, Physical Sciences, Math, CS) ESTIMATED TOTAL IN 2016 SINCE 1970: 5,309,239 TOTAL FROM 2001 to 2015 (Science and Engineering Indicators 2018) 2,429,300 ESTIMATED FUTURE STUDENTS (2016 to 2026): 2,565,802 ANNUAL GROWTH RATE: 2.88 % US POPULATION GROWTH RATE (2016): 0.7 % STUDENTS PASSING AP CALCULUS EXAM ESTIMATED TOTAL IN 2016 SINCE 1970: 5,045,848 TOTAL FROM 2002 to 2016 (College Board) 3,038,279 ESTIMATED FUTURE STUDENTS (2016 to 2026): 4,199,602 ANNUAL GROWTH RATE: 5.53 % US POPULATION GROWTH RATE (2016): 0.7 % estimate_college_stem.py ALL DONE
The table below gives the raw numbers from Figure 02-10 in the NSF Science and Engineering Indicators 2018 report with a column for total STEM degrees and a column for total STEM degrees in hard science and technology subjects (Engineering, Computer Science, Mathematics, and Physical Sciences) added for clarity:
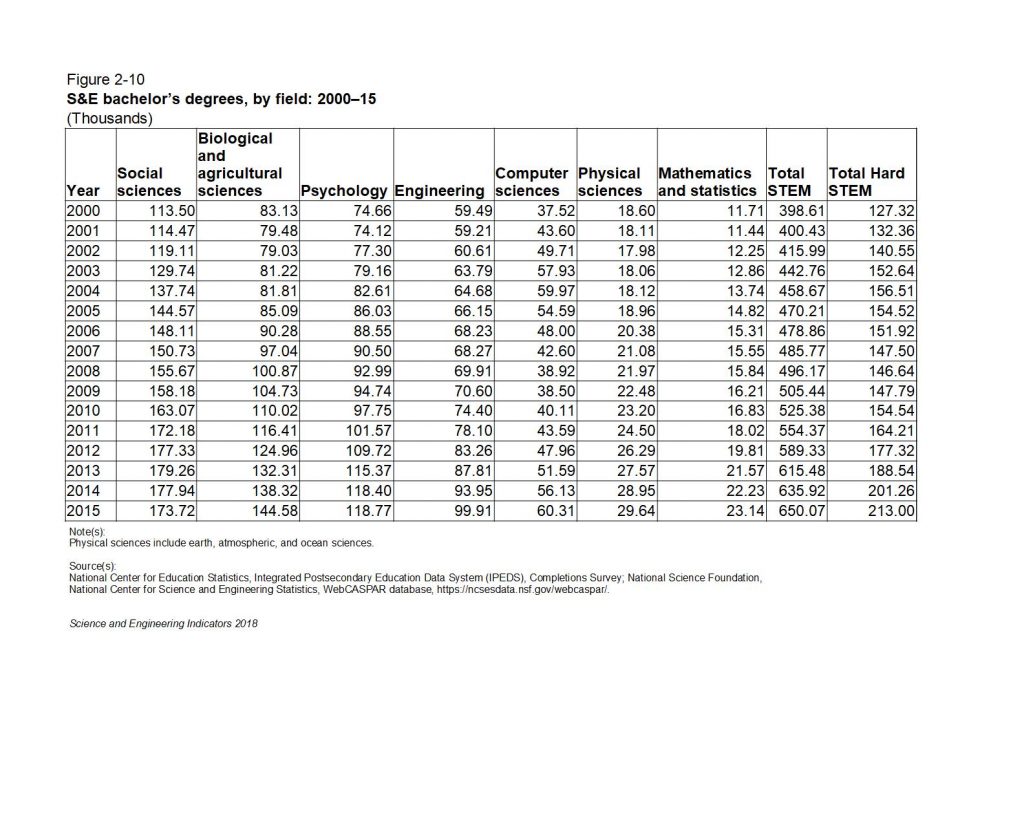
In the raw numbers, we see steady growth in social science and psychology STEM degrees from 2000 to 2015 with no obvious sign of the Internet/dot com bubble. There is a slight drop in Biological and agricultural sciences degrees in the early 00s. Somewhat larger drops can be seen in Engineering and Physical Sciences degrees in the early 00’s as well as a concomittant sharp rise in Computer Science (CS) degrees. This probably reflects strong STEM students shifting into CS degrees.
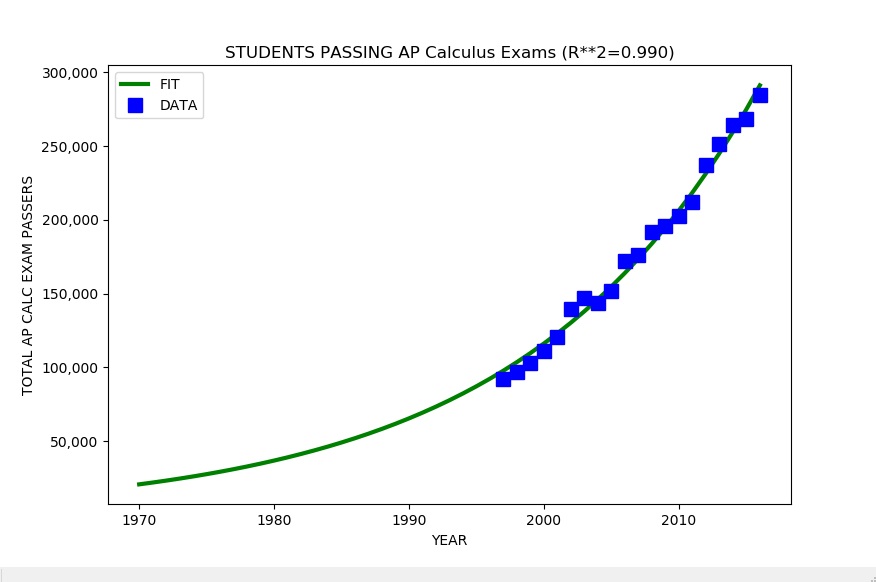
The number of K-12 students taking and passing the AP Calculus Exam (either the AB or more advanced BC exam) grows continuously and rapidly during the entire period from 1997 to 2016, growing at over five percent per year, far above the United States population growth rate of 0.7 percent per year.
The number of college students earning hard STEM degrees appears to be slightly smaller than the four year lagged number of K-12 students passing the AP exam, suggesting some attrition of strong STEM students at the college level. We might expect the number of hard STEM bachelors degrees granted each year to be the same or very close to the number of AP Exam passing students four years earlier.
A model using only the hard STEM bachelors degree students gives a total number of STEM college students produced since 1970 of five million, pretty close to the number of K-12 students estimated from the AP Calculus exam data. This is somewhat less than the 6.9 million total employed STEM workers estimated by the United States Bureau of Labor Statistics.
Including all STEM degrees gives a huge surplus of STEM students/workers, most not employed in a STEM field as reported by the US Census and numerous media reports.
The hard STEM degree model predicts about 2.5 million new STEM workers graduating between 2016 and 2026. This is slightly more than the number of STEM job openings seemingly predicted by the Bureau of Labor Statistics (about 800,000 new STEM jobs and about 1.5 million retirements and deaths of current aging STEM workers giving a total of about 2.3 million “new” jobs). The AP student model predicts about 4 million new STEM workers, far exceeding the BLS predictions and most other STEM employment predictions.
The data and models do not include the effects of immigration and guest worker programs such as the controversial H1-B visa, L1 visa, OPT visa, and O (“Genius”) visa. Immigrants and guest workers play an outsized role in the STEM labor force and specifically in the computer science/software labor force (estimated at 3-4 million workers, over half of the STEM labor force).
Difficulty of Evaluating “Soft” STEM Degrees
Social science, psychology, biological and agricultural sciences STEM degrees vary widely in rigor and technical requirements. The pioneering statistician Ronald Fisher developed many of his famous methods as an agricultural researcher at the Rothamsted agricultural research institute. The leading data analysis tool SAS from the SAS Institute was originally developed by agricultural researchers at North Carolina State University. IBM’s SPSS (Statistics Package for Social Sciences) data analysis tool, number three in the market, was developed for social sciences. Many “hard” sciences such as experimental particle physics use methods developed by Fisher and other agricultural and social scientists. Nonetheless, many “soft” science STEM degrees do not involve the same level of quantitative, logical, and programming skills typical of “hard” STEM fields.
In general, STEM degrees at the college level are not highly standardized. There is no national or international standard test or tests comparable to the AP Calculus exams at the K-12 level to get a good national estimate of the number of qualified students.
The numbers suggest but do not prove that most K-12 students who take and pass AP Calculus continue on to hard STEM degrees or some type of rigorous biology or agricultural sciences degree — hence the slight drop in biology and agricultural science degrees during the dot com bubble period with students shifting to CS degrees.
Conclusion
Both the college “hard” STEM degree data and the K-12 AP Calculus exam data strongly suggest that the United States can and will produce more qualified STEM students than job openings predicted for the 2016 to 2026 period. Somewhat more according to the college data, much more according to the AP exam data, and a huge surplus if all STEM degrees including psychology and social science are considered. The data and models do not include the substantial number of immigrants and guest workers in STEM jobs in the United States.
NOTE: The raw data in text CSV (comma separated values) format and the Python analysis program are included in the appendix below.
(C) 2018 by John F. McGowan, Ph.D.
About Me
John F. McGowan, Ph.D. solves problems using mathematics and mathematical software, including developing gesture recognition for touch devices, video compression and speech recognition technologies. He has extensive experience developing software in C, C++, MATLAB, Python, Visual Basic and many other programming languages. He has been a Visiting Scholar at HP Labs developing computer vision algorithms and software for mobile devices. He has worked as a contractor at NASA Ames Research Center involved in the research and development of image and video processing algorithms and technology. He has published articles on the origin and evolution of life, the exploration of Mars (anticipating the discovery of methane on Mars), and cheap access to space. He has a Ph.D. in physics from the University of Illinois at Urbana-Champaign and a B.S. in physics from the California Institute of Technology (Caltech).
Appendix: Source Code and Raw Data
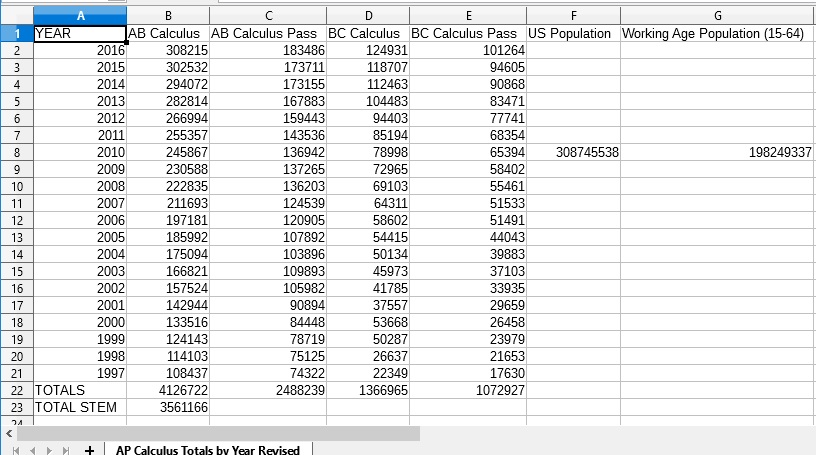
AP Calculus Totals.csv
Year,Total 2016.0,284750.0 2015.0,268316.0 2014.0,264023.0 2013.0,251354.0 2012.0,237184.0 2011.0,211890.0 2010.0,202336.0 2009.0,195667.0 2008.0,191664.0 2007.0,176072.0 2006.0,172396.0 2005.0,151935.0 2004.0,143779.0 2003.0,146996.0 2002.0,139917.0
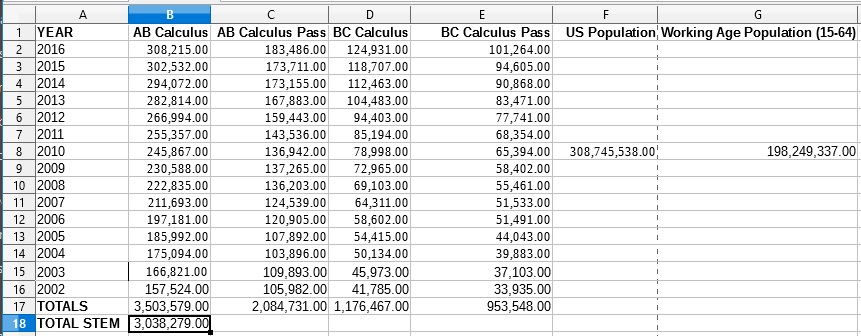
STEM Degrees with Totals.csv
Year,Social sciences,Biological and agricultural sciences,Psychology,Engineering,Computer sciences,Physical sciences,Mathematics and statistics,Total STEM,Total Hard STEM 2000,113.50,83.13,74.66,59.49,37.52,18.60,11.71,398.61,127.32 2001,114.47,79.48,74.12,59.21,43.60,18.11,11.44,400.43,132.36 2002,119.11,79.03,77.30,60.61,49.71,17.98,12.25,415.99,140.55 2003,129.74,81.22,79.16,63.79,57.93,18.06,12.86,442.76,152.64 2004,137.74,81.81,82.61,64.68,59.97,18.12,13.74,458.67,156.51 2005,144.57,85.09,86.03,66.15,54.59,18.96,14.82,470.21,154.52 2006,148.11,90.28,88.55,68.23,48.00,20.38,15.31,478.86,151.92 2007,150.73,97.04,90.50,68.27,42.60,21.08,15.55,485.77,147.50 2008,155.67,100.87,92.99,69.91,38.92,21.97,15.84,496.17,146.64 2009,158.18,104.73,94.74,70.60,38.50,22.48,16.21,505.44,147.79 2010,163.07,110.02,97.75,74.40,40.11,23.20,16.83,525.38,154.54 2011,172.18,116.41,101.57,78.10,43.59,24.50,18.02,554.37,164.21 2012,177.33,124.96,109.72,83.26,47.96,26.29,19.81,589.33,177.32 2013,179.26,132.31,115.37,87.81,51.59,27.57,21.57,615.48,188.54 2014,177.94,138.32,118.40,93.95,56.13,28.95,22.23,635.92,201.26 2015,173.72,144.58,118.77,99.91,60.31,29.64,23.14,650.07,213.00
estimate_college_stem.py
#
# Estimate the total production of STEM students at the
# College level from BS degrees granted (United States)
#
# (C) 2018 by John F. McGowan, Ph.D. (ceo@mathematical-software.com)
#
# Python standard libraries
import os
import sys
import time
# Numerical/Scientific Python libraries
import numpy as np
import scipy.optimize as opt # curve_fit()
import pandas as pd # reading text CSV files etc.
# Graphics
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from mpl_toolkits.mplot3d import Axes3D
# customize fonts
SMALL_SIZE = 8
MEDIUM_SIZE = 10
LARGE_SIZE = 12
XL_SIZE = 14
XXL_SIZE = 16
plt.rc('font', size=XL_SIZE) # controls default text sizes
plt.rc('axes', titlesize=XL_SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=XL_SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=XL_SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=XL_SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=XL_SIZE) # legend fontsize
plt.rc('figure', titlesize=XL_SIZE) # fontsize of the figure title
# STEM Bachelors Degrees earned by year (about 2000 to 2015)
#
# data from National Science Foundation (NSF)/ National Science Board
# Science and Engineering Indicators 2018 Report
# https://www.nsf.gov/statistics/2018/nsb20181/
# Figure 02-10
#
input_file = "STEM Degrees with Totals.csv"
if len(sys.argv) > 1:
index = 1
while index < len(sys.argv):
if sys.argv[index] in ["-i", "-input"]:
input_file = sys.argv[index+1]
index += 1
elif sys.argv[index] in ["-h", "--help", "-help", "-?"]:
print("Usage:", sys.argv[0], " -i input_file='AP Calculus Totals by Year.csv'")
sys.exit(0)
index +=1
print(__file__, "started", time.ctime()) # time stamp
print("Processing data from: ", input_file)
# read text CSV file (exported from spreadsheet)
df = pd.read_csv(input_file)
# drop NaNs for missing values in Pandas
df.dropna()
# get number of students who pass AP Calculus Exam (AB or BC)
# each year
df_ap_pass = pd.read_csv("AP Calculus Totals.csv")
ap_year = df_ap_pass.values[:,0]
ap_total = df_ap_pass.values[:,1]
# numerical data
hard_stem_str = df.values[1:,-1] # engineering, physical sciences, math/stat, CS
all_stem_str = df.values[1:,-2] # includes social science, psychology, agriculture etc.
hard_stem = np.zeros(hard_stem_str.shape)
all_stem = np.zeros(all_stem_str.shape)
for index, val in enumerate(hard_stem_str.ravel()):
if isinstance(val, str):
hard_stem[index] = np.float(val.replace(',',''))
elif isinstance(val, (float, np.float)):
hard_stem[index] = val
else:
raise TypeError("unsupported type " + str(type(val)))
for index, val in enumerate(all_stem_str.ravel()):
if isinstance(val, str):
all_stem[index] = np.float(val.replace(',', ''))
elif isinstance(val, (float, np.float)):
all_stem[index] = val
else:
raise TypeError("unsupported type " + str(type(val)))
DEGREES_PER_UNIT = 1000
# units are thousands of degrees granted
all_stem = DEGREES_PER_UNIT*all_stem
hard_stem = DEGREES_PER_UNIT*hard_stem
years_str = df.values[1:,0]
years = np.zeros(years_str.shape)
for index, val in enumerate(years_str.ravel()):
years[index] = np.float(val)
# almost everyone in the labor force graduated since 1970
# someone 18 years old in 1970 is 66 today (2018)
START_YEAR = 1970
def my_exp(x, *p):
"""
exponential model for curve_fit(...)
"""
return p[0]*np.exp(p[1]*(x - START_YEAR))
# starting guess for model parameters
p_start = [ 50000.0, 0.01 ]
# fit all STEM degree data
popt, pcov = opt.curve_fit(my_exp, years, all_stem, p_start)
# fit hard STEM degree data
popt_hard_stem, pcov_hard_stem = opt.curve_fit(my_exp, \
years, \
hard_stem, \
p_start)
# fit AP Students data
popt_ap, pcov_ap = opt.curve_fit(my_exp, \
ap_year, \
ap_total, \
p_start)
print(popt) # sanity check
STOP_YEAR = 2016
NYEARS = (STOP_YEAR - START_YEAR + 1)
years_fit = np.linspace(START_YEAR, STOP_YEAR, NYEARS)
n_fit = my_exp(years_fit, *popt)
n_pred = my_exp(years, *popt)
r2 = 1.0 - (n_pred - all_stem).var()/all_stem.var()
r2_str = "%4.3f" % r2
n_fit_hard = my_exp(years_fit, *popt_hard_stem)
n_pred_hard = my_exp(years, *popt_hard_stem)
r2_hard = 1.0 - (n_pred_hard - hard_stem).var()/hard_stem.var()
r2_hard_str = "%4.3f" % r2_hard
n_fit_ap = my_exp(years_fit, *popt_ap)
n_pred_ap = my_exp(ap_year, *popt_ap)
r2_ap = 1.0 - (n_pred_ap - ap_total).var()/ap_total.var()
r2_ap_str = "%4.3f" % r2_ap
cum_all_stem = n_fit.sum()
cum_hard_stem = n_fit_hard.sum()
cum_ap_stem = n_fit_ap.sum()
# to match BLS projections
future_years = np.linspace(2016, 2026, 11)
assert future_years.size == 11 # sanity check
future_students = my_exp(future_years, *popt)
future_students_hard = my_exp(future_years, *popt_hard_stem)
future_students_ap = my_exp(future_years, *popt_ap)
# https://fas.org/sgp/crs/misc/R43061.pdf
#
# The U.S. Science and Engineering Workforce: Recent, Current,
# and Projected Employment, Wages, and Unemployment
#
# by John F. Sargent Jr.
# Specialist in Science and Technology Policy
# November 2, 2017
#
# Congressional Research Service 7-5700 www.crs.gov R43061
#
# "In 2016, there were 6.9 million scientists and engineers (as
# defined in this report) employed in the United States, accounting
# for 4.9 % of total U.S. employment."
#
# BLS astonishing/bizarre projections for 2016-2026
# "The Bureau of Labor Statistics (BLS) projects that the number of S&E
# jobs will grow by 853,600 between 2016 and 2026 , a growth rate
# (1.1 % CAGR) that is somewhat faster than that of the overall
# workforce ( 0.7 %). In addition, BLS projects that 5.179 million
# scientists and engineers will be needed due to labor force exits and
# occupational transfers (referred to collectively as occupational
# separations ). BLS projects the total number of openings in S&E due to growth ,
# labor force exits, and occupational transfers between 2016 and 2026 to be
# 6.033 million, including 3.477 million in the computer occupations and
# 1.265 million in the engineering occupations."
# NOTE: This appears to project 5.170/6.9 or 75 percent!!!! of current STEM
# labor force LEAVE THE STEM PROFESSIONS by 2026!!!!
# "{:,}".format(value) to specify the comma separated thousands format
#
print("TOTAL Scientists and Engineers 2016:", "{:,.0f}".format(6.9e6))
# ALL STEM
print("\nALL STEM Bachelor's Degrees")
print("ESTIMATED TOTAL IN 2016 SINCE ", START_YEAR, ": ", \
"{:,.0f}".format(cum_all_stem), sep='')
# don't use comma grouping for years
print("TOTAL FROM", "{:.0f}".format(years_str[0]), \
"to 2015 (Science and Engineering Indicators 2018) ", \
"{:,.0f}".format(all_stem.sum()))
print("ESTIMATED FUTURE STUDENTS (2016 to 2026):", \
"{:,.0f}".format(future_students.sum()))
# annual growth rate of students taking AP Calculus
growth_rate_pct = (np.exp(popt[1]) - 1.0)*100
print("ANNUAL GROWTH RATE: ", "{:,.2f}".format(growth_rate_pct), \
"% US POPULATION GROWTH RATE (2016): 0.7 %")
# HARD STEM
print("\nHARD STEM DEGREES ONLY (Engineering, Physical Sciences, Math, CS)")
print("ESTIMATED TOTAL IN 2016 SINCE ", START_YEAR, ": ", \
"{:,.0f}".format(cum_hard_stem), sep='')
# don't use comma grouping for years
print("TOTAL FROM", "{:.0f}".format(years_str[0]), \
"to 2015 (Science and Engineering Indicators 2018) ", \
"{:,.0f}".format(hard_stem.sum()))
print("ESTIMATED FUTURE STUDENTS (2016 to 2026):", \
"{:,.0f}".format(future_students_hard.sum()))
# annual growth rate of students taking AP Calculus
growth_rate_pct_hard = (np.exp(popt_hard_stem[1]) - 1.0)*100
print("ANNUAL GROWTH RATE: ", "{:,.2f}".format(growth_rate_pct_hard), \
"% US POPULATION GROWTH RATE (2016): 0.7 %")
# AP STEM -- Students passing AP Calculus Exam Each Year
print("\nSTUDENTS PASSING AP CALCULUS EXAM")
print("ESTIMATED TOTAL IN 2016 SINCE ", START_YEAR, ": ", \
"{:,.0f}".format(cum_ap_stem), sep='')
# don't use comma grouping for years
print("TOTAL FROM", "{:.0f}".format(ap_year[-1]), \
"to", "{:.0f}".format(ap_year[0])," (College Board) ", \
"{:,.0f}".format(ap_total.sum()))
print("ESTIMATED FUTURE STUDENTS (2016 to 2026):", \
"{:,.0f}".format(future_students_ap.sum()))
# annual growth rate of students taking AP Calculus
growth_rate_pct_ap = (np.exp(popt_ap[1]) - 1.0)*100
print("ANNUAL GROWTH RATE: ", "{:,.2f}".format(growth_rate_pct_ap), \
"% US POPULATION GROWTH RATE (2016): 0.7 %")
# US Census reports 0.7 percent annual growth of US population in 2016
# SOURCE: https://www.census.gov/newsroom/press-releases/2016/cb16-214.html
#
f1 = plt.figure(figsize=(12,9))
ax = plt.gca()
# add commas to tick values (e.g. 1,000 instead of 1000)
ax.get_yaxis().set_major_formatter(
ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
DOT_COM_CRASH = 2000.25 # usually dated march 10, 2000
OCT_2008_CRASH = 2008.75 # usually dated October 11, 2008
DELTA_LABEL_YEARS = 0.5
plt.plot(years_fit, n_fit, 'g', linewidth=3, label='ALL STEM FIT')
plt.plot(years, all_stem, 'bs', markersize=10, label='ALL STEM DATA')
plt.plot(years_fit, n_fit_hard, 'r', linewidth=3, label='HARD STEM FIT')
plt.plot(years, hard_stem, 'ms', markersize=10, label='HARD STEM DATA')
plt.plot(years_fit, n_fit_ap, 'k', linewidth=3, label='AP STEM FIT')
plt.plot(ap_year, ap_total, 'cd', markersize=10, label='AP STEM DATA')
[ylow, yhigh] = plt.ylim()
dy = yhigh - ylow
# add marker lines for crashes
plt.plot((DOT_COM_CRASH, DOT_COM_CRASH), (ylow+0.1*dy, yhigh), 'b-')
plt.text(DOT_COM_CRASH + DELTA_LABEL_YEARS, 0.9*yhigh, '<-- DOT COM CRASH')
# plt.arrow(...) add arrow (arrow does not render correctly)
plt.plot((OCT_2008_CRASH, OCT_2008_CRASH), (ylow+0.1*dy, 0.8*yhigh), 'b-')
plt.text(OCT_2008_CRASH+DELTA_LABEL_YEARS, 0.5*yhigh, '<-- 2008 CRASH')
plt.legend()
plt.title('STUDENTS STEM BACHELORS DEGREES (ALL R**2=' \
+ r2_str + ', HARD R**2=' + r2_hard_str + \
', AP R**2=' + r2_ap_str + ')')
plt.xlabel('YEAR')
plt.ylabel('TOTAL STEM BS DEGREES')
# appear to need to do this after the plots
# to get valid ranges
[xlow, xhigh] = plt.xlim()
[ylow, yhigh] = plt.ylim()
dx = xhigh - xlow
dy = yhigh - ylow
# put input data file name in lower right corner
plt.text(xlow + 0.65*dx, \
ylow + 0.05*dy, \
input_file, \
bbox=dict(facecolor='red', alpha=0.2))
plt.show()
f1.savefig('College_STEM_Degrees.jpg')
print(__file__, "ALL DONE")